Il livello data link del modello ISO/OSI

In questo articolo, Il livello data link del modello ISO/OSI, analizziamo il secondo livello dello stack che si occupa di offrire ai livelli superiori la possibilità di inviare dati senza preoccuparsi dell’hardware di rete e dei problemi di interfacciamento al mezzo fisico

Indice dei contenuti

Introduzione al livello Data Link

Il livello Data Link si occupa di consegnare il contenuto informativo da un punto A a un punto B (comunicazione punto-punto) con A e B nodi della rete fisicamente collegati.

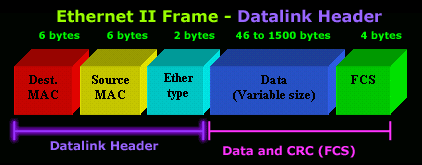
In fase di invio riceve il pacchetto dal livello Network, inserisce un header (intestazione) di livello 2 e un trailer (una coda) definendo il FRAME (trama) che sarà poi inviato al livello fisico.

In fase di ricezione, riceve i bit dal livello fisico, riconosce inizio e fine FRAME, elimina intestazione e coda del livello fisico e invia il frame al livello Network

È il livello che, attraverso i propri protocolli, garantisce:

• Framing: formattazione dei bit
• Controllo del flusso: per la sincronizzazione tra mittente e ricevente
• Rilevazione errori in fase di trasmissione

Ed, inoltre, definisce precise regole di comunicazione tra i due nodi. La comunicazione avvene attraverso 3 fasi:

• Apertura: i nodi A e B attraverso l’handshake iniziale si mettono d’accordo su come sincronizzare la comunicazione
• Mantenimento: fase di comunicazione regolata dal controllo del flusso
• Chiusura: fine della comunicazione

---

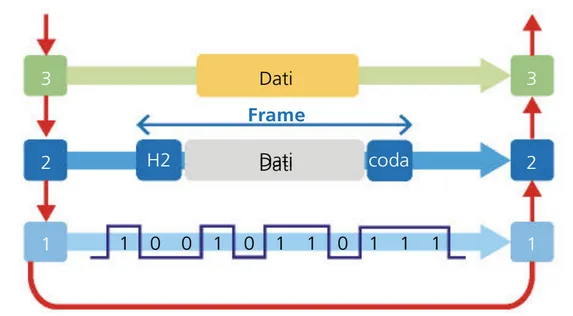
Framing

Il framing consiste nella definizione della struttura del flusso di bit in frame (trame). Ogni frame è costituito da:

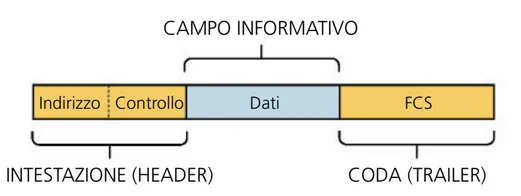
• Header: contenente tra le altre informazioni gli indirizzi fisici del mittente e del destinatario ed un campo di controllo.
• Payload: campo informativo
• Trailer: bit ridondanti utili alla rilevazione di errori in fase di trasmissione

Esistono diverse tecniche che consentono di delimitare una trama ma le più comunemente utilizzate sono:

• character stuffing: questa tecnica si usa nella trasmissione orientata al byte (la trama mantiene la suddivisione in byte). Il frame viene preceduto dalla sequenza di caratteri ASCII DLE STX (Data Link Escape Start of TeXt) e finisce con la sequenza DLE ETX (Data Link Escape End of TeXt). Se un frame si rovina e la destinazione perde la sincronizzazione basta trovare il successivo DLE STX o DLE ETX. Il carattere DLE però può comparire casualmente dentro al frame; perché questi caratteri non interferiscano viene aggiunto un ulteriore DLE (che viene rimosso a destinazione prima di passare al frame al livello di rete) in modo che solo i DLE singoli vengano interpretati come delimitatori; questa tecnica si chiama character stuffing
• bit stuffing: ogni frame inizia e finisce con la sequenza 01111110 chiamata flag: questa sequenza può comparire casualmente nei dati, perciò in trasmissione dopo cinque 1 consecutivi viene sempre inserito uno 0 nel flusso di bit, indipendentemente dal fatto che il bit successivo sia 1 o 0, mentre in ricezione bisogna provvedere ad eliminare i bit inseriti, rimuovendo sempre uno 0 dopo cinque 1; questa tecnica è chiamata bit stuffing

Controllo errori in trasmissione

Per la gestione degli errori in fase di trasmissione si utilizzano dei bit di ridondanza che vengono aggiunti al trailer. Esistono diverse tecniche in base alle quali è possibile solo rilevare gli errori in fase di trasmissione senza correggerli ed altre tecniche che consentono sia la rilevazione che la correzione degli errori

Tecniche di rilevazione degli errori

Controllo di parità

Prevede l’aggiunta di un bit ridondante ai dati, calcolato a seconda che il numero di bit che valgono 1 sia pari o dispari. I bit di parità è uno dei codici di rilevazione più semplici.

Ci sono due varianti del bit di parità:

• bit di parità pari (EVEN): si pone tale bit uguale a 1 se il numero di “1” in un certo insieme di bit è dispari (facendo diventare il numero totale di “1”, incluso il bit di parità, pari).
• bit di parità dispari (ODD): si pone tale bit uguale a 1 se il numero di “1” in un certo insieme di bit è pari (facendo diventare il numero totale di “1”, incluso il bit di parità, dispari)

Esempio: il valore della parità calcolato da B corrisponde con il valore del bit di parità aspettato -> nessun errore

Esempio: Il valore della parità calcolato da B (1) non è in accordo con il bit (0) che ha ricevuto –> errore in fase di trasmissione

Il bit di parità garantisce di rilevare solo un numero dispari di errori. Se avviene un numero pari di errori, non funziona. Si consideri il seguente esempio con un numero di errori pari:

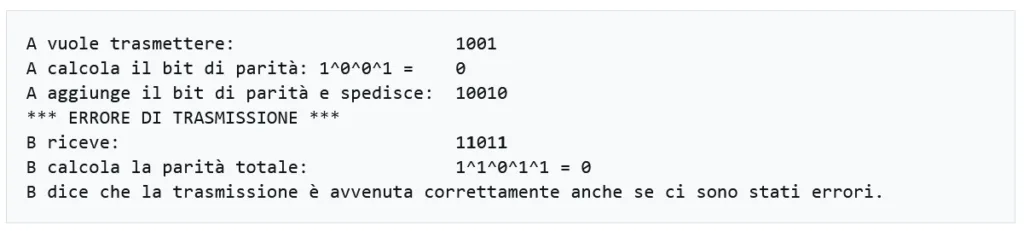
B osserva una parità pari, come aspettato, e quindi fallisce nel cercare due errori

Per la sua semplicità, la parità è usata in molti dispositivi hardware dove le operazioni possono essere ripetute in caso di difficoltà, o se è solo utile sapere che è avvenuto un errore. Per esempio i bus SCSI e PCI usano la parità per trovare errori di trasmissione, inoltre molte cache di microprocessori includono tale sistema di protezione. In definitiva la tecnica è usata per trasmissioni seriali asincrone a bassa velocità e a breve distanza.

---

Checksum

Consiste nel sommare il valore binario corrispondente alla codifica ASCII dei
caratteri, modulo 256. Lato mittente viene fatto il complemento bit a bit della
somma di tutti i caratteri del frame; se c’è un riporto finale, questo è sommato al
bit meno significativo. Il risultato è posto nel campo di controllo apposito (se il
campo è a 16 bit si sommano parole di 16 bit).

---

Controllo a ridondanza ciclica (CRC – Ciclic Redundancy Check)

Il CRC prevede la generazione di una stringa di bit di controllo che viene normalmente trasmessa assieme ai dati e il calcolo è basato sull’aritmetica modulare. Un codice CRC è definito dal suo polinomio generatore: ad esempio il codice CRC-16-CCITT, molto usato in ambito di telecomunicazioni, è definito dal polinomio generatore x ¹⁶ + x ¹² + x ⁵ + 1 .

Il calcolo del CRC inizia con il messaggio che viene associato a un polinomio b(x) di grado pari al numero di bit del messaggio meno uno, grado che indicheremo con
(n −1)

Per esempio, il messaggio 10011010 ( n − 1 = 7 ) produce il polinomio

b (x) = x ⁷ + x ⁴ + x ³ + x ¹ poichè i bit a 1 corrispondono ai coefficienti del polinomio b(x)

L’algoritmo prevede di:

• convertire il polinomio generatore in sequenza di bit
• aggiungere in coda al messaggio da trasmettere tanti zeri corrispondenti al grado del polinomio generatore
• eseguire la divisione XOR tra il nuovo messaggio e la sequenza relativa al polinomio generatore
• il resto della divisione rappresenta il CRC e va accodato al messaggio originario che verrà poi trasmesso

Il ricevente può effettuare il controllo in due modi: il primo consiste nel dividere
tutto il messaggio ricevuto, compreso il resto della divisione, per il polinomio
generatore: se il resto della divisione è 0, allora il messaggio è corretto. Il secondo
modo consiste nell’eliminare il resto della divisione dai dati ricevuti e dividerlo
per il polinomio generatore: se il resto ottenuto è uguale a quello tolto dai dati
ricevuti, allora il messaggio è corretto

Tecniche di correzione dell’errore

Combinazione di Vertical redundancy check (VRC) e Longitudinal redundancy check, LRC

Il controllo di ridondanza longitudinale o controllo di ridondanza orizzontale (HRC) è una forma di controllo di ridondanza che si applica indipendentemente a ciascuno dei gruppi paralleli di bit di un flusso dati. I dati devono essere divisi in blocchi di trasmissione, ai quali il blocco di controllo addizionale viene accodato

In un sistema con controllo bidimensionale di parità (combinazione di VRC e LRC), il messaggio trasmesso comprende:

1. I bit di dati (organizzati in una matrice: righe × colonne),
2. I bit di parità per ogni riga (VRC),
3. I bit di parità per ogni colonna (LRC), che costituiscono una riga aggiuntiva.

In sostanza, si trasmette una matrice estesa, in cui:

Alla fine delle righe si aggiunge una riga di parità LRC, che ha i bit di parità di colonna e il bit di parità finale di se stesso.

Ogni riga di dati ha un bit di parità finale.

Supponiamo di voler trasmettere i seguenti 4 nibble: 1011 0100 1101 0011

Il messaggio vene riorganizzato in una matrice 4 x 4 in cui i 4 nibble sono le righe:

Righe → / Colonne ↓	Bit1	Bit2	Bit3	Bit4
R1	1	0	1	1
R2	0	1	0	0
R3	1	1	0	1
R4	0	0	1	1

A questo punto si calcolano i bit di parità pari per ogni riga aggiungendo i bit di VRC:

Righe / Colonne	B1	B2	B3	B4	Parità riga
R1	1	0	1	1	1
R2	0	1	0	0	1
R3	1	1	0	1	1
R4	0	0	1	1	0

Ora si calcolano i bit di parità di ogni colonna aggiungendo la quinta riga LRC:

Righe / Colonne	B1	B2	B3	B4	Parità riga
R1	1	0	1	1	1
R2	0	1	0	0	1
R3	1	1	0	1	1
R4	0	0	1	1	0
LRC	0	0	0	1	1

Il messaggio trasmesso sarà: 10111 01001 11011 00110 00011

In fase di ricezione supponendo un errore in trasmissione sul bit 2 della riga 2 (da 1 a 0) il ricevente vedrà: 10111 00001 11011 00110 00011. Strutturerà la matrice per righe:

Righe / Colonne	B1	B2	B3	B4	Parità riga
R1	1	0	1	1	1
R2	0	0	0	0	1
R3	1	1	0	1	1
R4	0	0	1	1	0
LRC	0	0	0	1	1

e calcolerà i bit di parità di riga che saranno: 10101 e i bit di parità di colonna 01011.

Li confronterà con i bit di parità ricevuti e capirà che nella posizione (2,2) c’è stato un errore per cui modificherà il valore di quel bit

Codici di Hamming

È un codice lineare che aggiunge dei bit di parità ai dati, calcolati in modo tale da poter determinare esattamente la posizione del bit errato in caso di errore singolo.

La tecnica prevede di calcolare e posizionare i bit di ridondanza nelle posizioni che corrispondono alle potenze del 2.

Dato il messaggio da trasmettere costituito da m bit, la tecnica prevede di calcolare i k bit di ridondanza in modo da inviare un messaggio n di lunghezza m+k che è chiamato codeword.

il numero k di bit di ridondanza si ottiene per tentativi risolvendo la disequazione:

2^k – 1 >= m+k.

Se ad esempio m=4 -> k = 3

Il codice di Hamming standard è noto come (7,4):

• 4 bit di dati
• 3 bit di parità
• Totale: 7 bit trasmessi

Nei 7 bit, i bit di parità sono posizionati nelle posizioni che sono potenze di 2:
(1, 2, 4)

Ecco la struttura del codice Hamming (7,4):

Posizione	1	2	3	4	5	6	7
Tipo	P1	P2	D1	P4	D2	D3	D4

Esempio: invio del messaggio D = 1 0 1 1 (D1, D2, D3, D4)

Posizioniamo i bit:

Posizione	1	2	3	4	5	6	7
Contenuto	?	?	1	?	0	1	1

Vediamo quali bit sono controllati dai bit di ridondanza

Posizione	Codifica	Controllo
1	001	3,5,7
2	010	3,6,7
3	011	–
4	100	5,6,7
5	101	–
6	110	–
7	111	–

Quindi:

• P1 controlla: 3, 5, 7
• P2 controlla: 3, 6, 7
• P4 controlla: 5, 6, 7

Calcolo dei bit di parità:

P1 (controlla 3, 5, 7):

→ XOR di 1 (pos 3), 0 (pos 5), 1 (pos 7):
1 ⊕ 0 ⊕ 1 = 0 -> quindi il bit in posizione 1 avrà valore 0

P2 (controlla 3, 6, 7):

→ XOR di 1 (pos 3), 1 (pos 6), 1 (pos 7):
1 ⊕ 1 ⊕ 1 = 1 -> quindi il bit in posizione 2 avrà valore 1

P4 (controlla 5, 6, 7):

→ XOR di 0 (pos 5), 1 (pos 6), 1 (pos 7):
0 ⊕ 1 ⊕ 1 = 0 -> quindi il bit in posizione 4 avrà valore 0

Messaggio trasmesso:

Posizione	1	2	3	4	5	6	7
Contenuto	0	1	1	0	0	1	1

Messaggio Trasmesso: 0110011

Simuliamo un errore: bit n.5 (da 0 a 1)

Messaggio Ricevuto: 0110111

Ricalcolo delle parità ricevute:

Controllo P1 (1,3,5,7):

1 (3) ⊕ 1 (5) ⊕ 1 (7) = 1 ⊕ 1 = 0, 0 ⊕ 1 = 1

→ Parità non corretta → P1 = 1

Controllo P2 (2,3,6,7):

1 (2) ⊕ 1 (3) ⊕ 1 (6) ⊕ 1 (7) = 1 ⊕ 1 = 0, 0 ⊕ 1 = 1, 1 ⊕ 1 = 0

→ Parità corretta → P2 = 0

Controllo P4 (4,5,6,7):

0 (4) ⊕ 1 (5) ⊕ 1 (6) ⊕ 1 (7) = 0 ⊕ 1 = 1, 1 ⊕ 1 = 0, 0 ⊕ 1 = 1

→ Parità corretta → P4 = 1

Rileggendo le parità nell’ordine inverso (P4,P2,P1) -> 101 -> convertito in decimale da 5 -> errore in posizione 5

Controllo del flusso

Il controllo del flusso consiste nella regolazione delle velocità del flusso dei
dati dal trasmettitore al ricevitore. È utilizzato dalla stazione ricevente per in-
formare la sorgente del suo stato ed evitare di essere sommersa dalle trame che
le arrivano.

Il ricevitore, con un meccanismo di retroazione, è in grado di regolare il flusso
dei dati, assicurando che il ritmo con cui il trasmettitore inoltra le trame sul ca-
nale non ecceda quello con cui il ricevitore può riceverle ed elaborarle, evitando
di mandare in overflow il buffer del ricevitore con la conseguente perdita di dati.
È realizzato con due tecniche:

• ARQ – Automatic Repeat-reQuest, il trasmettitore deve attendere la conferma
  di una trama prima di inviare la successiva;
• finestra scorrevole (sliding window), in cui il ricevitore dà il permesso al
  trasmettitore di inviare dati fino al raggiungimento della capacità massima
  del buffer di memoria.

La prima tecnica viene utilizzata nei protocolli di livello accesso alla rete dello stack TCP/IP (protocollo HDLC e protocollo PPP)

La seconda tecnica viene utilizzata nel protocollo LLC di IEEE 802 (che studieremo in seguito) definito a livello accesso alla rete dello stack TCP/IP, nel protocollo HDLC e nel protocollo TCP (che studieremo in seguito) definito a livello trasporto dello stack TCP/IP

Tecnica PAR (Positive Acknowledgement and Retry)

E’ una tecnica basata su ARQ. Garantisce che ogni frame inviato sia stato ricevuto correttamente. Se il mittente non riceve conferma (acknowledgement), ritrasmette il frame.

Funzionamento

Il processo si ripete finché il frame non viene confermato.

Il mittente invia un frame al destinatario.

Il destinatario verifica l’integrità del frame (ad es. tramite CRC). Se il frame è corretto, invia un acknowledgement (ACK). Se ha riscontrato errori invia un Not Acknoledgement (NACK) per esempio se al messaggio originario si e’ sovrapposto rumore elettromagnetico modificando il valore di qualche bit.

Se il mittente non riceve l’ACK entro un certo timeout, ritrasmette il frame.

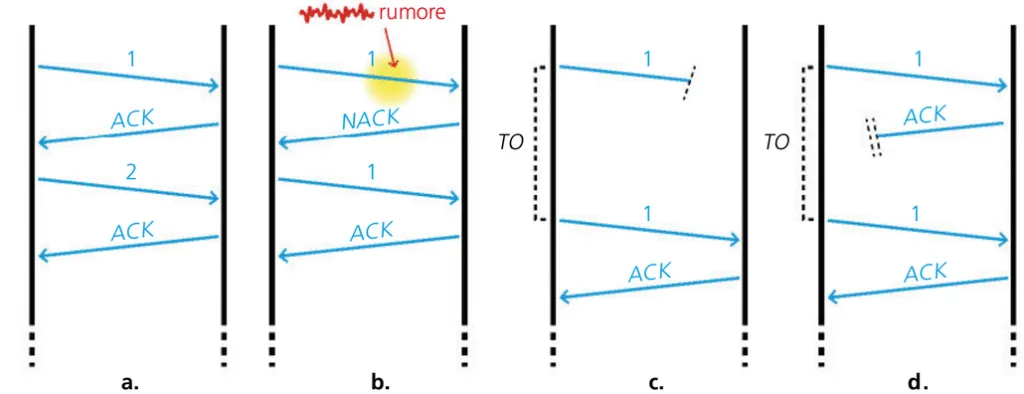
a. Trasmissione senza errori

b. Trasmissione con rumore nella trama 1 -> ritrasmissione della trama 1

c. Timeout in fase di invio della trama 1–> ritrasmissione trama 1

d. Timeout in fase di ricezione ACK –> ritrasmissione rama 1

Questo metodo è semplice, ma inefficiente per collegamenti con latenza alta o larghezza di banda elevata, poiché invia un solo frame alla volta.

Tecnica Sliding Window

Lo scopo di questa tecnica è quello di ottimizzare la trasmissione permettendo di inviare più frame prima di ricevere conferma, e gestire l’ordine dei dati.

Concetti chiave

• Il mittente può inviare più frame consecutivamente, fino a un numero massimo chiamato dimensione della finestra (window size).
• Detto N il numoro di trame trasmesse e K il numero di trame confermate in ricezione deve risultare che W>=N-K con W = larghezza della finestra
• Ogni frame ha un numero di sequenza.
• Il destinatario invia ACK per i frame ricevuti correttamente.
• Se un frame è danneggiato o manca, viene ritrasmesso.
• Dopo la conferma la finestra si sposta verso destra

Le tecniche di error recovery (per il recupero degli errori in trasmissione) avviene con le tecniche:

• Go-Back-N: in caso di errore si ritrasmettono tutti i frame successivi
• Selective Repeat: si ritrasmettono solo i frame errati

---

---

---

---